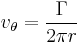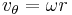Vortex
A vortex (plural: vortices) is a spinning, often turbulent, flow of fluid. Any spiral motion with closed streamlines is vortex flow. The motion of the fluid swirling rapidly around a center is called a vortex. The speed and rate of rotation of the fluid in a free (irrotational) vortex are greatest at the center, and decrease progressively with distance from the center, whereas the speed of a forced (rotational) vortex is zero at the center and increases proportional to the distance from the center. Both types of vortices exhibit a pressure minimum at the center, though the pressure minimum in a free vortex is much lower.
Contents |
Properties
Vortices display some special properties:
- The fluid pressure in a vortex is lowest in the center and rises progressively with distance from the center. This is in accordance with Bernoulli's Principle. The core of a vortex in air is sometimes visible because of a plume of water vapor caused by condensation in the low pressure of the core. The spout of a tornado is a classic and frightening example of the visible core of a vortex. A dust devil is also the core of a vortex, made visible by the dust drawn upwards by the turbulent flow of air from ground level into the low pressure core.
- The core of every vortex can be considered to contain a vortex line, and every particle in the vortex can be considered to be circulating around the vortex line. Vortex lines can start and end at the boundary of the fluid or form closed loops. They cannot start or end in the fluid. (See Helmholtz's theorems.) Vortices readily deflect and attach themselves to a solid surface. For example, a vortex usually forms ahead of the propeller disk or jet engine of a slow-moving airplane. One end of the vortex line is attached to the propeller disk or jet engine, but when the airplane is taxiing the other end of the vortex line readily attaches itself to the ground rather than end in midair. The vortex can suck water and small stones into the core and then into the propeller disk or jet engine.
- Two or more vortices that are approximately parallel and circulating in the same direction will merge to form a single vortex. The circulation of the merged vortex will equal the sum of the circulations of the constituent vortices. For example, a sheet of small vortices flows from the trailing edge of the wing or propeller of an airplane when the wing is developing lift or the propeller is developing thrust. In less than one wing chord downstream of the trailing edge of the wing these small vortices merge to form a single vortex. If viewed from the tail of the airplane, looking forward in the direction of flight, there is one wingtip vortex trailing from the left-hand wing and circulating clockwise, and another wingtip vortex trailing from the right-hand wing and circulating anti-clockwise. The result is a region of downwash behind the wing, between the pair of wingtip vortices. These two wingtip vortices do not merge because they are circulating in opposite directions.
- Vortices contain a lot of energy in the circular motion of the fluid. In an ideal fluid this energy can never be dissipated and the vortex would persist forever. However, real fluids exhibit viscosity and this dissipates energy very slowly from the core of the vortex. (See Rankine vortex). It is only through dissipation of a vortex due to viscosity that a vortex line can end in the fluid, rather than at the boundary of the fluid. For example, the wingtip vortices from an airplane dissipate slowly and linger in the atmosphere long after the airplane has passed. This is a hazard to other aircraft and is known as wake turbulence.
Dynamics
A vortex can be any circular or rotary flow. Perhaps unexpectedly, not all vortices possess vorticity. Vorticity is a mathematical concept used in fluid dynamics. It can be related to the amount of "circulation" or "rotation" in a fluid. In fluid dynamics, vorticity is the circulation per unit area at a point in the flow field. It is a vector quantity, whose direction is (roughly speaking) along the axis of the swirl. The vorticity of a free vortex is zero everywhere except at the center, whereas the vorticity of a forced vortex is non-zero. Vorticity is an approximately conserved quantity, meaning that it is not readily created or destroyed in a flow. Therefore, flows that start with minimal vorticity, such as water in a basin, create vortices with minimal vorticity, such as the characteristic swirling and approximately free vortex structure when it drains. By contrast, fluids that initially have vorticity, such as water in a rotating bowl, form vortices with vorticity, exhibited by the much less pronounced low pressure region at the center of this flow. Also in fluid dynamics, the movement of a fluid can be said to be vortical if the fluid moves around in a circle, or in a helix, or if it tends to spin around some axis. Such motion can also be called solenoidal. In the atmospheric sciences, vorticity is a property that characterizes large-scale rotation of air masses. Since the atmospheric circulation is nearly horizontal, the (3 dimensional) vorticity is nearly vertical, and it is common to use the vertical component as a scalar vorticity. Mathematically, vorticity 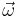 is defined as the curl of the fluid velocity
is defined as the curl of the fluid velocity 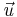 :
:
Two types of vortex
In fluid mechanics, a distinction is often made between two limiting vortex cases. One is called the free (irrotational) vortex, and the other is the forced (rotational) vortex. These are considered below, using the following example:
| Reference position in a counter-clockwise vortex. | In an irrotational vortex, the leaves preserve their original orientation while moving counter-clockwise. | In a rotational vortex, the leaves rotate with the counter-clockwise flow. |
Free (irrotational) vortex
When fluid is drawn down a plug-hole, one can observe the phenomenon of a free vortex or line vortex. The tangential velocity v varies inversely as the distance r from the center of rotation, so the angular momentum rv is uniform everywhere throughout the flow; the vorticity is zero everywhere (except for a singularity at the center-line) and the circulation about a contour containing r = 0 has the same value everywhere.[1] The free surface (if present) dips sharply (as r −2 ) as the center line is approached.
The tangential velocity is given by:
where Γ is the circulation and r is the radial distance from the center of the vortex.
In non-technical terms, the fluid near the center of the vortex circulates faster than the fluid far from the center. The speed along the circular path of flow decreases as you move out from the center. At the same time the inner streamlines have a shorter distance to travel to complete a ring. If you were running a race on a circular track would you rather be on the inside or outside, assuming the goal was to complete a circle? Imagine a leaf floating in a free vortex. The leaf's tip points to the center and the blade straddles multiple streamlines. The outer flow is slow in terms of angle traversed and it exerts a backwards tug on the base of the leaf while the faster inner flow pulls the tip forwards. The drag force opposes rotation of the leaf as it moves around the circle.
Forced (rotational) vortex
In a forced vortex the fluid rotates as a solid body (there is no shear). The motion can be realized by placing a dish of fluid on a turntable rotating at ω radian/s; the fluid has vorticity of 2ω everywhere, and the free surface (if present) is a paraboloid.
The tangential velocity is given by:[1]
where ω is the angular velocity and r is the radial distance from the center of the vortex.
Vortices in magnets
Different classes of vortex waves also exist in magnets. There are exact solutions to classical nonlinear magnetic equations e.g. Landau-Lifshitz equation, continuum Heisenberg model, Ishimori equation, nonlinear Schrödinger equation and so on.
Observations
A vortex can be seen in the spiraling motion of air or liquid around a center of rotation. The circular current of water of conflicting tides often form vortex shapes. Turbulent flow makes many vortices. A good example of a vortex is the atmospheric phenomenon of a whirlwind or a tornado or dust devil. This whirling air mass mostly takes the form of a helix, column, or spiral. Tornadoes develop from severe thunderstorms, usually spawned from squall lines and supercell thunderstorms, though they sometimes happen as a result of a hurricane.
In atmospheric physics, a mesovortex is on the scale of a few miles (smaller than a hurricane but larger than a tornado). [2] On a much smaller scale, a vortex is usually formed as water goes down a drain, as in a sink or a toilet. This occurs in water as the revolving mass forms a whirlpool. This whirlpool is caused by water flowing out of a small opening in the bottom of a basin or reservoir. This swirling flow structure within a region of fluid flow opens downward from the water surface.
Instances
- In the hydrodynamic interpretation of the behaviour of electromagnetic fields, the acceleration of electric fluid in a particular direction creates a positive vortex of magnetic fluid. This in turn creates around itself a corresponding negative vortex of electric fluid.
- Smoke ring : A ring of smoke that persists for a surprisingly long time, illustrating the slow rate at which viscosity dissipates the energy of a vortex.
- Bubble ring : A ring of bubbles formed under water, moving in any direction, created by some playful dolphins and other whales.
- Lift-induced drag of a wing on an aircraft.
- The primary cause of drag in the sail of a sloop.
- Whirlpool: a swirling body of water produced by ocean tides or by a hole underneath the vortex where the water would drain out, such as a bathtub. A large, powerful whirlpool is known as a maelstrom. In popular imagination, but only rarely in reality, they can have the dangerous effect of destroying boats. Examples are Charybdis of classical mythology in the Straits of Messina, Italy; the Naruto whirlpools of Nankaido, Japan; the Maelstrom, Lofoten, Norway.
- Ice stalactites are formed by a rotating column of downward-moving supercooled brine.
- A small stream of falling water starts rotating immediately on release and does so until the speed of downward movement overcomes the cohesion of surface tension and causes its breakup into spray.
- Tornado : a violent windstorm characterized by a twisting, funnel-shaped cloud. A less violent version of a tornado, over water, is called a waterspout.
- Hurricane : a much larger, swirling body of clouds produced by evaporating warm ocean water and influenced by the Earth's rotation. Similar, but far greater, vortices are also seen on other planets, such as the permanent Great Red Spot on Jupiter and the intermittent Great Dark Spot on Neptune.
- Polar vortex : a persistent, large-scale cyclone centered near the Earth's poles, in the middle and upper troposphere and the stratosphere.
- Sunspot : dark region on the Sun's surface (photosphere) marked by a lower temperature than its surroundings, and intense magnetic activity.
- The accretion disk of a black hole or other massive gravitational source.
- Spiral galaxy : a type of galaxy in the Hubble sequence that is characterized by a thin, rotating disk. Earth's galaxy, the Milky Way, is of this type.
See also
- Artificial gravity
- Batchelor vortex
- Cyclonic separation
- Eddy
- Gyre
- Helmholtz's theorems
- History of fluid mechanics
- Horseshoe vortex
- Quantum vortex
- Rankine vortex
- Shower-curtain effect
- Strouhal number
- Viktor Schauberger
- Vile Vortices
- Von Kármán vortex street
- Vortex engine
- Vortex ring
- Vortex tube
- Vortex cooler
- Vortex shedding
- Vortex stretching
- Vortex induced vibration
- Vorticity
- Whirlpool
- Wingtip vortices
- Wormhole
Notes
References and further reading
- "Weather Glossary"' The Weather Channel Interactive, Inc.. 2004.
- "Glossary and Abbreviations". Risk Prediction Initiative. The Bermuda Biological Station for Research, Inc.. St. George's, Bermuda. 2004.
- Loper, David E., "An analysis of confined magnetohydrodynamic vortex flows". Case Institute of Technology. Washington, National Aeronautics and Space Administration; for sale by the Clearinghouse for Federal Scientific and Technical Information, Springfield, Va. 1966. (NASA contractor report NASA CR-646) LCCN 67060315
- Batchelor, G. K. (1967), An Introduction to Fluid Dynamics, Cambridge Univ. Press, Ch. 7 et seq
- Clancy, L.J. (1975), Aerodynamics, Pitman Publishing Limited, London. ISBN 0 273 01120 0
External links
- Optical Vortices
- Create Vortex
- Dust Devil Movie A short movie showing many spinning vortices of varying sizes
- Video of two water vortex rings colliding (MPEG)
- BubbleRings.com Web site on "bubble rings", which are underwater rings made of air formed from vortices. The site has some information on how these rings work.
- Chapter 3 Rotational Flows: Circulation and Turbulence
- Video of Vortex Formation and Annihilation in a Superconductor (By Joel Thorarinson)